Den Mantel und die Oberfläche eines Kegels praktisch erschließen: Ein Einblick in den Matheunterricht im Jahrgang 10
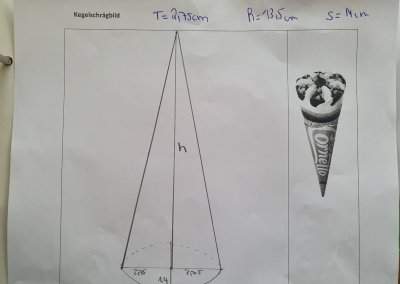
So macht Matheunterricht Spaß: Mithilfe eines Cornetto – Eis erforschten die Schülerinnen und Schüler bei Mathekollegin Vanessa Mues den Mantel und die Oberfläche eines Kegels. Das Waffeleis weißt eine klassische Kegelform auf, bei dem die Jugendlichen zunächst Maß nehmen mussten: Den Radius r des Grundkreises, die Seitenkante des Eises sowie die Eishöhe h waren schnell gemessen.
Anschließend wickelten sie die Eisverpackung vorsichtig ab, damit sie nicht zerriss. Die zentrale Frage, die es nun galt zu beantworten, lautete: Aus welchen Teilen besteht die Verpackung? Die SchülerInnen fanden heraus, dass der Kreisausschnitt den Mantel und der kreisförmige Deckel die Grundfläche bildet und die Eisverpackung somit die Oberfläche des Kegels darstellt, also Kreisausschnitt + Kreis bzw. Mantel + Grundkreis. Nun konnten die SchülerInnen mithilfe der zuvor gemessenen Größen (Radius, Seitenkante und Höhe) den Mantel und die Oberfläche des Waffeleises berechnen und fertigten mithilfe der gemessenen Größen ein Schrägbild des Waffeleises an. Außerdem haben sich die Jugendlichen mithilfe eines Schüttversuchs die Formel zur Berechnung der Volumen hergeleitet. Wasser wird von einer Pyramide in einen Quader mit gleicher Grundfläche und gleicher Höhe geschüttet, um das Volumen der Pyramide zu bestimmen.
Dreimal kann die Flüssigkeit aus der Pyramide in den zugehörigen Quader gefüllt werden, also ist das Volumen einer Pyramide 1/3 des Volumens des zugehörigen Quaders. Der gleiche Versuch wird mit einem Kegel und einem Zylinder mit gleicher Grundfläche und gleicher Höhe durchgeführt. Hier kann ebenso dreimal die Flüssigkeit aus dem Kegel in einen zugehörigen Zylinder gefüllt werden. Wieder ergibt sich folgende Beziehung: Volumen Kegel = 1/3 Volumen Zylinder.
Und wer bei alledem besonders schnell war, der konnte sich das noch nicht geschmolzene Eis nach getaner Arbeit wohlverdient schmecken lassen :).